After some deliberation, I decided to use a design that allows the observer to move up and down between levels and features an interwoven system of vestibules (cells with six entries on each side, sort of like hallways) and regular cells (those that only have one entrance and exit and four walls) to create my library.

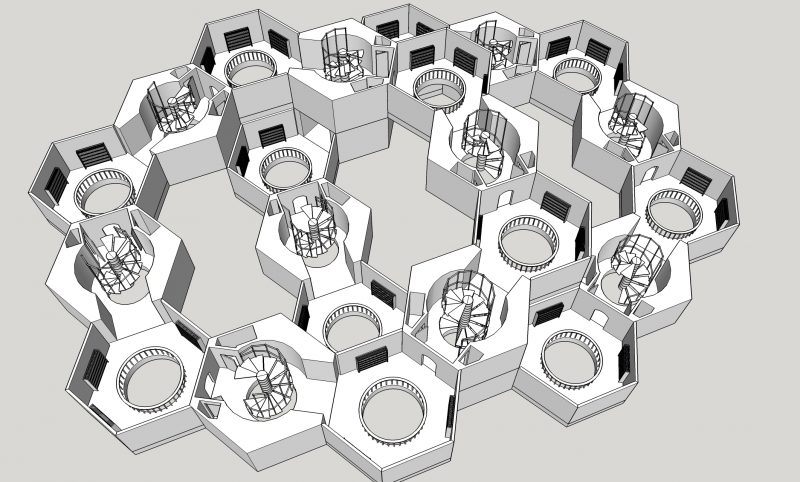
After some modeling, I had the following two models with baked-in lights along with packed 2K textures later on.

Before proceeding to integrate my models into the WebGL application, I needed to consider several critical factors.

Despite the future techniques I would employ to create the illusion of an infinite world, my immediate concern was to establish a system that would enable me to:

1. Construct a grid of interconnected hexagons.
2. Assign coordinates to these hexagons.
3. Perform arithmetic operations on these coordinates, such as retrieving neighboring cells.

An axial coordinate system, with an origin at zero, would suffice for this task.

Essentially, I would expand my coordinates in all directions (both positive and negative) from an origin cell located at Q: 0 and R: 0.With this system in place, I could take any point defined by Q and R and obtain neighboring cells by simply adding a vector of (Q, R) to the cell. Now, I was ready to begin generating the hexagonal pattern; however, there was one final consideration: the hexagon shape itself.

Hexagons are six-sided polygons — an obvious fact.

However, unlike a standard rectangular pattern where individual shapes can be tiled by precisely offsetting them according to their width and height, hexagons present a unique challenge. In the case of regular hexagons, where all sides are of equal length, the width does not equal the height, despite having a constant radius.

Observe how the width corresponds exactly to the radius of the encompassing circle, while the height does not.

The term "flat-top orientation" refers to a hexagon positioned with its flat side at the top and its pointed vertices oriented to the left and right. The opposite configuration is known as "pointy-top orientation."

As demonstrated above, the width can be calculated by simply doubling the radius. For my model, with a radius of 7, this results in a hexagon width of 14. The height, however, is derived by multiplying the radius by the square root of three, yielding approximately 12.12 for a radius of 7.

The final consideration involves the spacing of the hexagons, ensuring they can seamlessly form a grid. Simply offsetting them by their calculated width and height would not suffice, as this would fail to connect all sides and create gaps within the grid.



Armed with this information, I began to implement my HexUtility class in TypeScript, which included the following function to retrieve world positions from given axial coordinates, incorporating the necessary calculations outlined above for spacing.



The need to round the result of this calculation (hence the this.roundAxialHex(q, r) call) is crucial; without rounding, the function would return floating-point values for Q and R, merely translating world positions to axial coordinates without snapping them to the grid.



This leads to the following implementation in my class:

Thus, I was ready to dive into performing cheap magic tricks to create illusions of infinity...

Given the recurring pattern of cells — each consisting of a vestibule followed by a regular room — we can create an infinite loop by teleporting the observer back to the origin whenever they move more than two tiles away from it.



As illustrated by the image, when the observer is about to step onto any of the marked tiles, they are teleported back to the grey root cell.

However, simply teleporting the observer to the center of the root cell won't suffice, as it would break the illusion of continuity.

To preserve the illusion, the observer must be teleported to the opposite entrance within the grey origin, ensuring a seamless transition into a new room rather than simply reappearing in the center.

This process is also applied vertically. In this case, the observer is immediately looped back to the top when crossing into the next level, as the lower and upper levels are identical, allowing for a perfect vertical loop.

With that complete, the next step is to implement a first-person camera and a collision system, finally enabling navigation through the library...

As with most aspects of this project, and especially when it came to the implementation of the collision system, optimizing was a key priority.

The first and simplest optimization was leveraging the fact that the observer moves from cell to cell. By focusing collision checks exclusively on the current cell, we could eliminate unnecessary computations for cells that were outside the observer's immediate vicinity.

The next logical step was to incorporate a more sophisticated technique: a Bounding Volume Hierarchy (BVH) structure to further optimize performance.



In practical terms, we subdivide the space within each cell by grouping its geometric objects into smaller, manageable clusters. Each cluster is enclosed in a bounding volume. When the observer moves through the environment, we only check for collisions with the relevant bounding volumes rather than all the objects in the cell.

Here's how the process works: instead of checking every object in the cell for collisions, we first check if the observer enters one of the green bounding volumes which represent the volumes of the bounding volume hierarchy.

In an efficient BVH, nodes within any sub-tree should be spatially close to one another, with proximity increasing the deeper they are in the tree.

Each node should enclose its objects in the smallest possible volume, minimizing both the total sum of bounding volumes and the overlap between sibling nodes.

Greater focus should be placed on optimizing nodes closer to the root, as pruning these nodes excludes a larger number of objects from further checks. Additionally, maintaining a balanced tree structure ensures that non-relevant branches can be efficiently pruned during traversal.

Only if a collision with a bounding volume occurs will we perform the more expensive and precise collision detection on the objects contained within that volume. This drastically reduces the number of complex collision checks required.

For instance, the general collider structure for the cell is shown below. The floating shapes in the center represent elevators, which have their own responsive colliders.

Essentially, by organizing objects into a hierarchy of bounding volumes, we minimize the number of expensive collider checks. As the observer moves, we first check for collisions with the larger bounding volumes, which are computationally inexpensive.

Only if a collision is detected within these larger volumes do we proceed with a detailed collision check for the specific objects inside, which is far more resource-intensive.

This two-tier approach ensures smooth performance even in complex environments.

So far, we have created a grid of cells that appears infinite to the observer.

At the surface level, we are rendering a hexagonal cell pattern consisting of three rings around the origin. Currently, we are rendering the following:

It's clear that we are over-rendering a significant number of cells. The field of view only encompasses a portion of our grid, so we need to avoid rendering anything that lies outside this view.

As an initial step, we will implement frustum culling, an optimization technique that prevents the rendering of objects outside the field of view.

We will establish the frustum coordinates and use the bounding box of each cell to determine if it falls within the frustum.

However, we are still over-rendering certain cells.

If we recall the specific structure of our cells, which feature dedicated entrances and exits, we realize that walls lacking any openings can obstruct visibility to other cells.

For instance, consider the image below, where our field of view originates from the top left and flows through all marked cells.



The doors are marked as small boxes, and not all cells are visible from our position, even if they lie within the frustum.

Some cells are completely obstructed by walls to us due to not having any apparent entrance that we can use to look into them.

The optimization we will implement resembles occlusion culling, which prevents rendering of obstructed objects. To apply this method in our case, we will retrieve all doors from the current cell and traverse in the directions they lead. As we move through the cells accessible via the doors, we will inform our rendering engine to allow rendering of each encountered cell and subsequently retrieve the doors for this new cell, rendering only the next cell it connects to.

A crucial aspect of this approach is that we only deal with a subset of cells that were filtered out during the frustum culling so we can continue filtering. We want to avoid traversing cells that aren't even within the frustum, as that would make occlusion culling more costly than rendering without it.

By combining all these methods, we have successfully reduced our rendering from 37 cells per level to as few as 7 (in the best case) and 16 (in the worst case).

Our final rendering optimization will focus on geometry instancing.



Now, consider the following bookshelf.

That's a lot of books — 160 to be precise. With four walls in a cell containing 160 books each, we're looking at 640 individual objects per cell. When rendering multiple cells with these books, the number of objects increases further.

Even if the shape of an individual book is very simple, consisting of only eight vertices and twelve triangles, rendering so many books without optimization will likely prevent us from achieving our target of 60 frames per second on regular machines due to the high number of draw calls. The number of draw calls is often the most significant factor affecting performance.

This is where mesh instancing comes into play. To demonstrate its effectiveness, we can use the analogy of Blender's duplicate linked feature.

Note: Duplicate linked is not the same as instanced meshes; the former reduces memory consumption outside of rendering and may inadvertently enhance rendering performance, while the latter focuses on reducing draw calls by rendering multiple instances in a single call.

With that distinction in mind, consider the following two images:

Notice how, despite the second image containing more books, the geometry data (vertex, edges, faces, triangles) remains unchanged. This occurs because Blender copies over the data of the first book for each subsequent book in the editor.

Once we finalize this last optimization, our rendering process (more specifically WebGL's instanced rendering) will perform a similar operation by sending the geometry data of one book (vertices, normals, etc.) to the GPU in one go. It will then use a small set of additional data (like transformation matrices for position, rotation, and scale) to render multiple copies of that same geometry with different transformations in a single draw call, rather than repeating the entire geometry for each instance.

This approach will allow us to support many individual books while enabling users to highlight them by hovering over them with their mouse, as well as assign different colors to each book, keeping the bookshelf visually interesting.

With all the rendering handled and us looking at overall 60 frames per second, we now dive into the actual library content...

Consider this scenario: We have 29 unique characters (A-Z, comma, period, and space) that can form various strings on a page with a maximum length of 3200 characters.

This leads to an astronomical total of 29³²⁰⁰ unique pages in the library — roughly a 4000-digit number, vastly exceeding the number of atoms in the observable universe (estimated at 10⁸²). The question is: how do we map and retrieve such a vast quantity of pages efficiently?

Thankfully, we don't need to store or memorize every page. Just as we can compute certain values without storing all possible inputs, we can devise a procedure to generate and retrieve a specific page, as long as we know the key input, and in the case of reversing it, know the page's content (or a part of it).

The observer either wanders through the library (where we track movement) or performs a reverse search for a specific word. Thus, we either know the exact location of a page or its content (or part of its content), so we can optimize around those scenarios without storing every possible page.

Early in the development process, I considered using a reversible random number generator to generate pages. However, this approach proved unfeasible given the library's size — larger than the observable universe — and would have required brute-forcing or storing vast amounts of data.

Instead, I adopted an encoding and decoding scheme. With 26 letters plus the comma, period, and space, we have a 29-character set, so our page content can be represented in Base-29. For mapping locations, I chose a base64 encoding scheme to represent page identifiers efficiently.

Now, here's a simple encoding and decoding function:



This enables us to map a base64 identifier (representing the location of our page) to a Base-29 string (representing the page content).

But how do we generate identifiers? To simplify things, let's use integers. The number 0 corresponds to "a", the number 1 to "b", and so on. Once we exceed 29, we move to two-letter combinations like "aa", "ab", and so forth.

Our task is to create a function that can map integers from 0 to 29³²⁰⁰ into a string, which we can then encode in base64 for efficiency.

Next, how do we map a 3D location (like a cell's position in space) into a 1D number? One option is the Cantor pairing function.

However, since we're working in 3D, we need to adapt it either by applying it recursively or by using a different method that can handle three dimensions.

A simpler approach is to use a linear combination to flatten the 3D space into a 1D space by constructing a cube. To do this, we need to define the maximum size for each axis. Given the scale of the library, we can confidently say that no dimension (x, y, z) will require more space than the total number of pages in the library times two (to account for negative and positive coordinates). This constraint ensures that the cube's volume will be manageable.

However, not every mapped value on this axis needs as much space as the total number of pages, since a single cell contains multiple pages. So, we can shrink the cube by dividing the total number of pages in the library by the number of pages per cell.

Specifically, dividing 29³²⁰⁰ by the product of 640 (books per cell) and 410 (pages per book) gives us a much smaller axis size. This creates a more practical cube size for mapping cells.

To further optimize, we can reduce the space for negative and positive coordinates by calculating the perfect fit for each axis using the cube root function, adjusting for our earlier inflated axis size.

The final function for mapping a cell's Q, R, and level to a single number looks like this. AXIS_LENGTH is the calculated value, and AXIS_TOTAL_SIZE is twice that (for both positive and negative values). All values are offset by AXIS_LENGTH to avoid negative indices.



And here's the function to reverse this process and retrieve the original cell coordinates:



We can now combine this room number with additional numbers (e.g., the wall, shelf, volume, and page number within the cell) to create a unique identifier for each page’s location.



With all these components in place, we are ready to generate and reverse-map pages efficiently...

With nearly everything in place, the final piece was to implement a fully functional user interface to allow the observer to read books and reverse search through the library's vast collection.

The user interface is designed to be intuitive and easy to navigate, providing two primary functions:

• Browsing: Users can freely explore the library, turning through pages as they would in a real-world book, discovering randomly generated content across the entire collection.
• Reverse Search: Users can input a word or phrase to locate the exact page in the library where it appears, making the process of finding specific content effortless within the library's structure.

Despite the astronomical number of 29³²⁰⁰ possible pages, the interface streamlines navigation, allowing users to focus on exploration and discovery without being overwhelmed by the underlying complexity.

Below are snapshots of the final user interface:
The first interface showcases the browsing mode. It allows the observer to wander through the vast collection of books, flipping through pages one by one. The clean layout makes reading smooth and enjoyable, while navigation controls are placed intuitively for easy exploration.


In the second interface, we see the reverse search functionality. Here, the user can input specific words or phrases and instantly retrieve the page number and location within the library. This powerful search tool makes navigating the infinite library feel straightforward and efficient.


The third interface provides insights into the system's structure, showcasing the mapping between the abstract location and the content itself. This interface offers advanced users a glimpse into how each page is tied to a unique identifier within the vast library.

Now that everything is in place, the library is fully functional, allowing users to explore and locate any of the 29³²⁰⁰ unique pages across the entire collection!

You can start exploring the library here. I welcome any feedback or suggestions you may have as I continue to refine and expand this project. Thank you for your input!